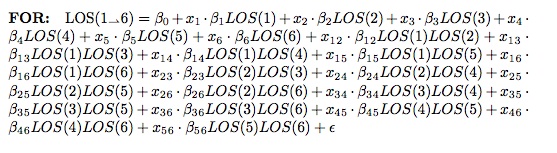Let’s go back to our care model expanded upon in our prior post. As eluded to, once interdependencies are considered, things get complicated fast. This might not be as apparent in our four-stage ER care delivery model, but consider a larger process with six stages, and each stage being able to interact with each other. See the figure below:
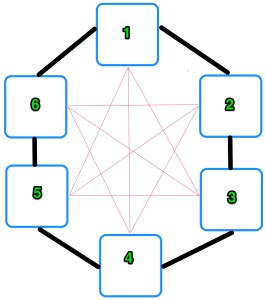For this figure, this is the generalized linear model with first order single interactions:
A 23 term generalized linear model is probably not going to really help anyone and is too unweildy, so something needs to be done to get to the heart of the matter and create a model which is reasonably simple and will well-approximate this process. The issue of multi-collinearity also is relevant here. So, the next step is to get the number of terms down to what matters. This would probably be best served by a shrinkage technique or a dimension reduction technique.
Shrinkage: The LASSO immediately comes to mind due to its coefficient minimization as a feature that may allow variable selection dependent on lambda. A ridge regression wouldn’t apply the same parsimony to the equation, so it keeps terms which may not help us simplify. It has been pointed out to me that there is a technique called elastic net regularization which combines features of both the LASSO and ridge regression – seems worth a look.
Dimension Reduction: First using Principal component analysis to identify the most important terms in the model and then utilizing Partial least squares to consider the response.
At this point, we probably have gone about as far as we can on a theoretical basis, and need to proceed on a more applied basis. That will be a subject of future posts.
Thanks to Flamdrag5 for clarifying my thoughts on this post.